Motor Control University
Embedded code implementation - Data Type
In digital hardware, numbers are then represented as either fixed-point or floating-point data types. Moveover Floating Point Unit (FPU), although more and more common, are not always present on chip (this is the case for the dsPIC33CK used in our example. Moreover, measurements from peripherals are integer, typically 12-bits resolution for the ADC. For reasons of efficiency, it may be useful to perform fixed-point conversions before converting data to floating-point. As mentioned in MathWorks article on Benefits of Fixed-Point Hardware, while floating-point processors can greatly simplify the real-time implementation of a control law the use of fixed-point data type is interesting for
- Size and Power Consumption - The logic circuits of fixed-point hardware are much less complicated than those of floating-point hardware. This means that the fixed-point chip size is smaller with less power consumption when compared with floating-point hardware.
- Memory Usage and Speed - In general fixed-point calculations require less memory and less processor time to perform.
- Cost - Fixed-point hardware is more cost effective where price/cost is an important consideration.
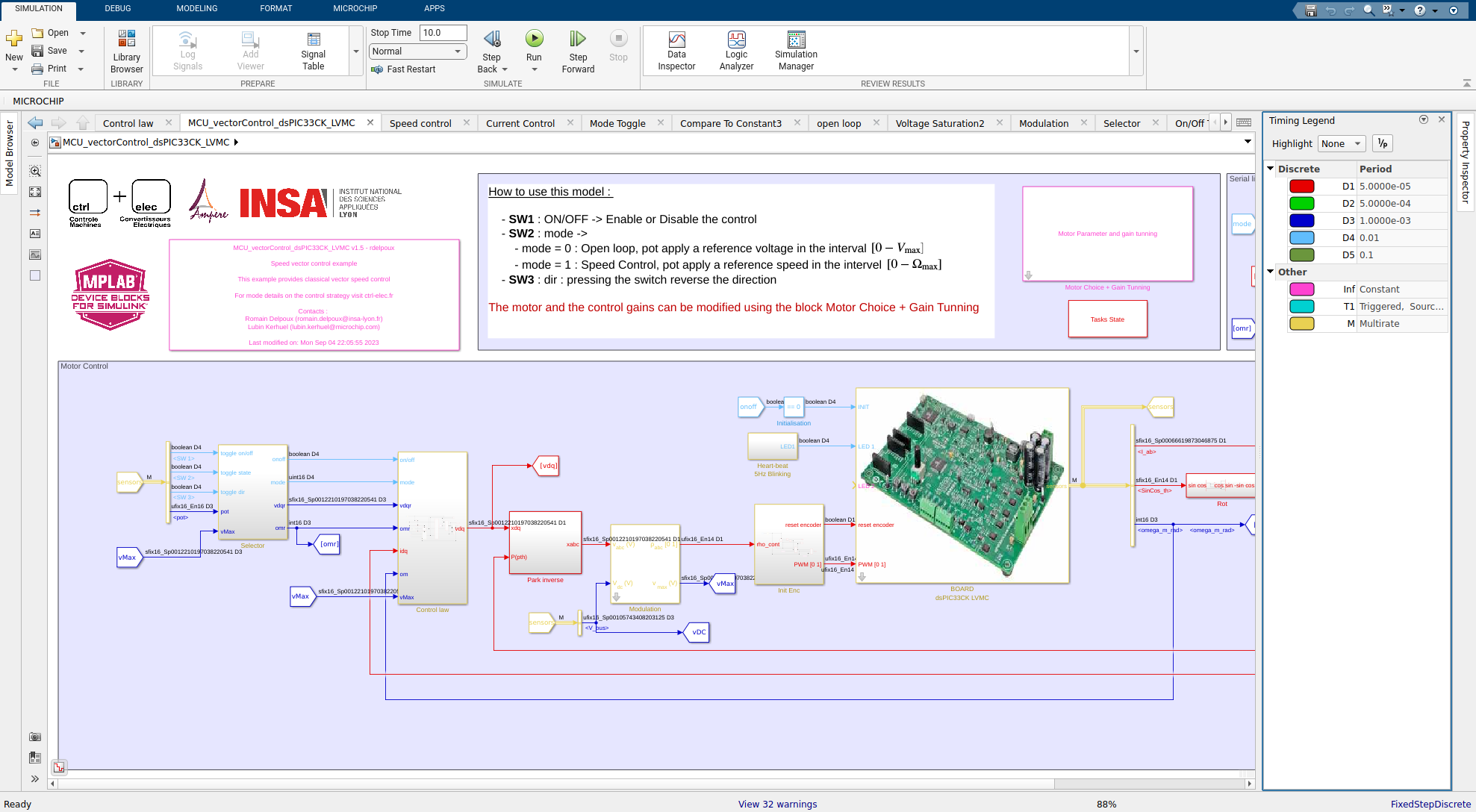
Embedded real-time code implementation requires thus a particular attention regarding the type of data used in the algorithm, specially for fastest tasks. In the proposed example (download from git), we have seen in real-time page that the code includes 5 discrete time tasks, with the fastest sampled at \(5\times10^{-5}\)s (\(20\)kHz), represented in red on the Simulink model.
Floating-point data types
A classical single precision floating point number is a 32-bits number with the flowing layout:
The relationship between single-precision format and the representation of real numbers is given by \[ value=(-1)^{\rm sign}\times2^{{\rm exponent}-127}\times {\rm fraction} \] The range, bias and precision for floating-point data are given below (from MathWorks Floating-point numbers):
| Data Type | Low Limit | High Limit | Exponent Bias | Precision |
|---|---|---|---|---|
| Half | \(2^{-14}\approx 6.1\times10^{-5}\) | \((2-2^{-10})\times 2^{15}\approx 6.5\times10^{4}\) | 15 | \(2^{-10}\approx 10^{-3}\) |
| Single | \(2^{-126}\approx 10^{-38}\) | \(2^{128}\approx3\times10^{38}\) | 127 | \(2^{-23}\approx 10^{-7}\) |
| Double | \(2^{-1022}\approx 2\times10^{-308}\) | \(2^{1024}\approx 2\times 10^{308}\) | 1023 | \(2^{-52}\approx 10^{-16}\) |
Fixed-point data types
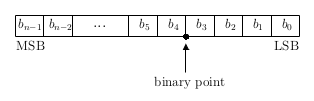
A binary representation of a generalized fixed-point number is shown below (from MathWorks Fixed-Point Data Types):
where:
- \(b_i\) is the \(i^{th}\) binary digit
- \(n\) is the word length
- \(b_{n-1}\) is the Most Significant Bit (MSB)
- \(b_0\) is the Least Significant bit (LSB)
In the example the binary point is shown four places to the left of the LSB. The number is said to have four fractional bits.
Fixed-point data types can be either signed or unsigned.
While embedded code can be designed using normalized values and omit the variables scaling for a better understanding of the control algorithm and keep physical interpretation of the variables used in the code, it is interesting to keep variable scaling. A particular attention is required using fixed-point data since the dynamic range of fixed-point values is much less than floating-point values with equivalent word sizes.
Fixed-point data types using Simulink
To fix scaling of the variables used in the code, Matlab/Simulink provides different data type notation and tools to facilitates the used of fixed-point data.
First an interesting is to be able to visualize the Base Data Type on the wire has shown on the figure:

The next figure shows different representation of the int16 number \(5555\):
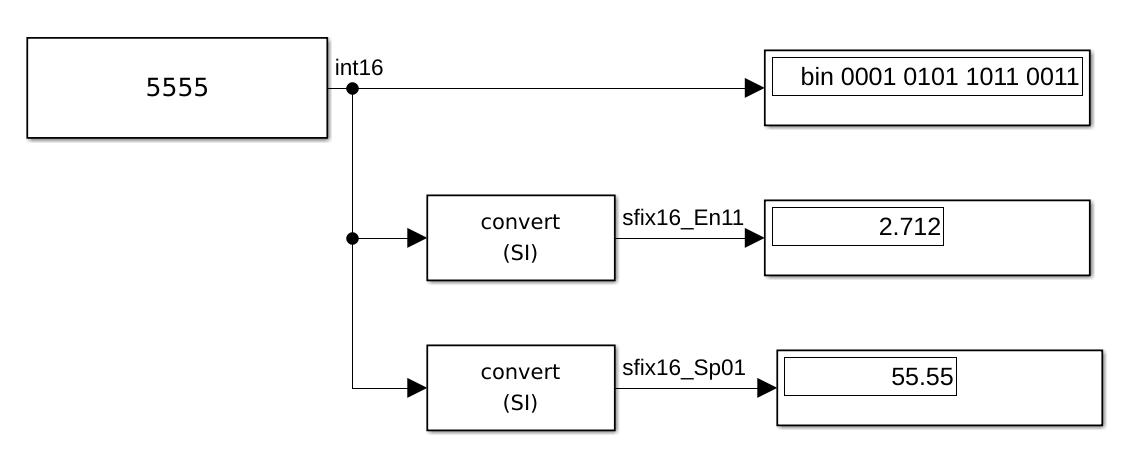
- \((5555)_{10} = (0001 0101 1011 0011)_2\)
- sfix16_EN11, scalling is En11, Exponent Negative \(2^{-11}\), the fraction length in this case corresponds to the \(11^{\rm th}\) LSB, which can be understand as:
\[ \begin{array}{cl} &&5555\times 2^{-11}\\ &=& (0001 0,101 1011 0011)_2\\ &=& 1\times2^1+1\times2^{-1}+1\times2^{-3}+1\times2^{-4}+1\times2^{-6}+1\times2^{-7}+1\times2^{-10}+1\times2^{-11}\\ &=& 2.712 \end{array} \]
For this configuration, the maximum value is \(15.99921171875\), and the precision corresponds to \(2^-11 \approx 4.8828\times10^{-4}\)
- sfix16_Sp01 has a slope of \(0.01\) is means that the LSB has a value of 0.01:
\[ \begin{array}{cl} &&5555\times 0.01\\ &=& (1\times2^{12}+1\times2^{10}+1\times2^{8}+1\times2^{7}+1\times2^{5}+1\times2^{4}+1\times2^{1}+1\times2^{0})\times0.01\\ &=& 55.55 \end{array} \]
- Stored Integer (SI) versus Real World Value (RWV)
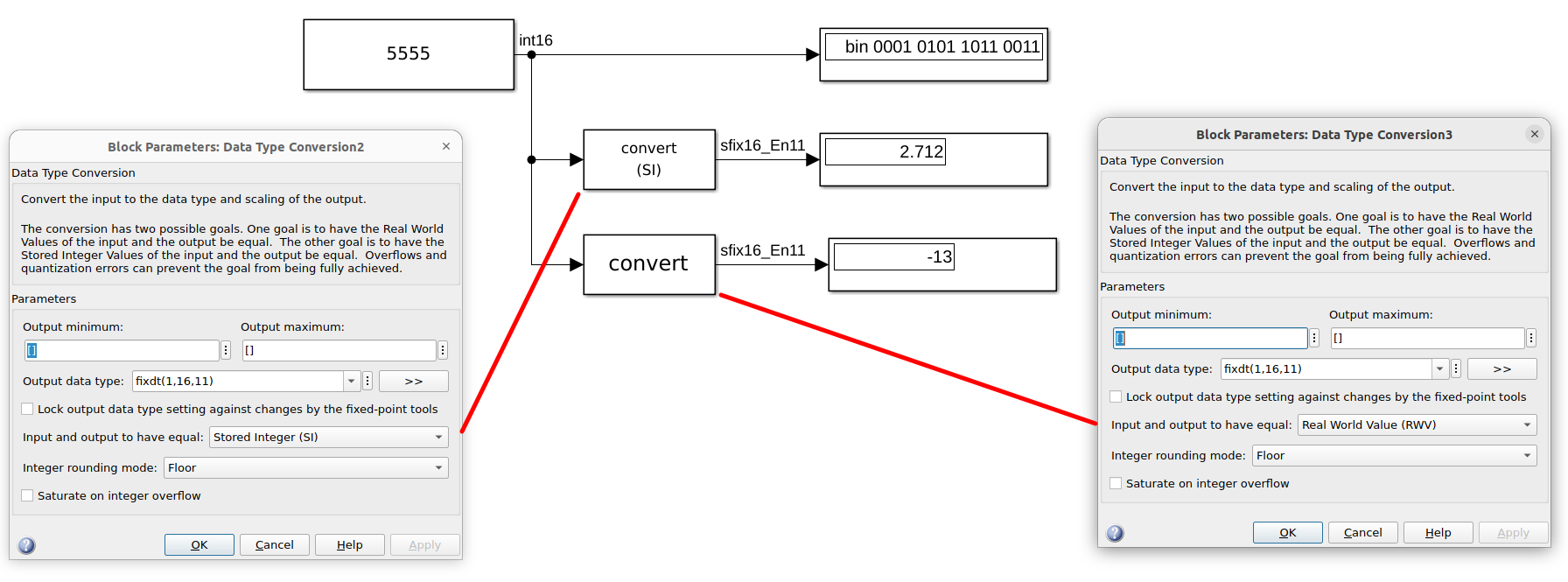
The Stored integer option (SI) takes the Integer \((0001 0101 1011 0011)_2\) and choses the binary point 11 places to the left of the LSB. The Real World Value (RWV) tries to convert the integer 5555 in the format sfix16_En11 while the maximum is \(16-2^{-11}\). Overflow occurs leading to the result \(-13\). Another option would be to saturate on integer overflow leading as result to the maximum representable number \(15.99951171875\)
Matlab/Simulink provides a tool for optimizing and implementing fixed-point algorithms.
" You can then test and debug quantization effects such as overflows and precision loss before implementing the design on hardware."
It requires however to have a good knowledge on the maximum and minimum values that all the variables of your algorithm may take which is not an easy task.
From the proposed example
In the proposed example (download from git), fixed point data type is used. Indeed, dsPIC33CK do not provides FPU.
- For current measurement, the output data type is chosen as : fixdt(1,16,21.83/32768,0). The DSC has ADC with 12 bits resolution and the current measurement ranges in \(\pm21.83\)A. In the ADC configuration block, the Conversion Format is chosen to be fractional (left aligned) which means that the maximum readable values from the ADC, for a signed 16 bits variable is \(2^{15}=32768\) corresponding to \(21.83\)A. The data type is chosen to have a slope equal to \(21.83/32768=6.662\times10^{-4}\). This data type choice allows to obtain current measurement, using fixed point data type with the best precision that the ADC can provide. The solution is used for the different ADC measurements.
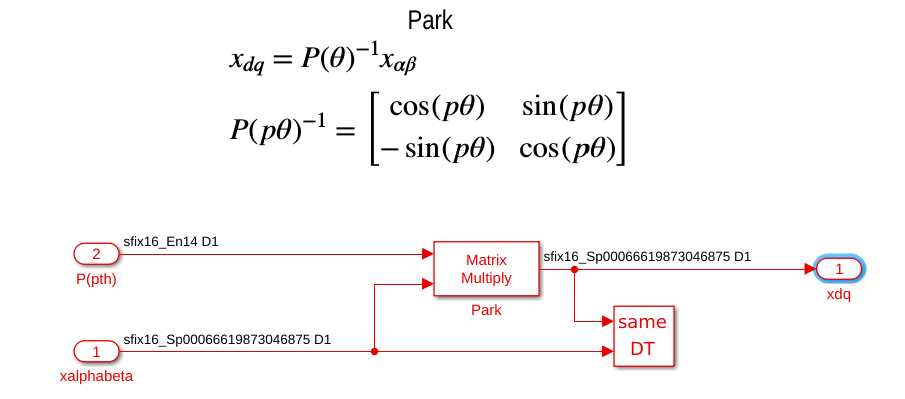
- It can be found in the model the Simulink block DataTypeDuplicate, for example in the Park transformation subsystem:
Knowing that Park’s transformation is a simple rotation (see transformation page), the norm of the variables at the input for the block is that same than the one at the output of the transformation. The current measurement is chosen to have a slope equal to \(6.662\times10^{-4}\) (corresponding to sfix16_sp000666198…) to maximize the measured current precision, then the output of the transformation will have the same precision. The DataTypeDuplicate block impose that the second input and output of the Matrix Multiply block to have the same data type.
- Another interesting block is the Data Type Propagation, used for example in the modulation subsystem:

Here, since DC voltage is always positive, the DC voltage is measured from the ADC with unsigned variable and the correct slope. In the modulation subsystem, the objective is to be able to represent the maximum voltage and thus scale the variables adequately without knowledge of the data type used for the DC voltage measurement. The voltages in the control algorithm ranges in \([-V_{\rm max}\quad V_{\rm max}] = \left[-\frac{V_{\rm DC}}{\sqrt{3}}\quad \frac{V_{\rm DC}}{\sqrt{3}}\right]\) for SVM (see modulation page) . The slope of the of variable is thus adjusted with a multiplicative adjustment of \(\frac{1}{\sqrt{3}}\) to have an output data type with the correct range and the best precision as possible.
References
- Fixed-point arithmetic, Wikipedia
- Fixed-Point Data Types, MathWorks Help Center
- Floating-point numbers, MathWorks Help Center
- Benefits of Fixed-Point Hardware, MathWorks Help Center

 GitHub
GitHub YouTube
YouTube
.png)
.png)