Motor Control University

Controller

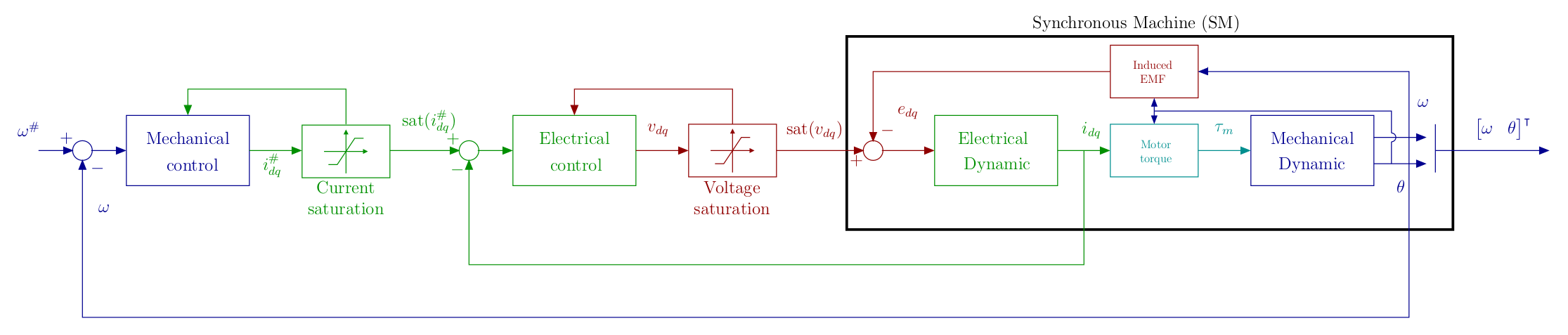
Based on the model described in the modeling page, and after Clarke et Park transformations described in the transformations page, in this page a dynamic control strategy is proposed. A classical cascaded vector control, based on the motor frequency separation (i.e. a fast electrical dynamics and a slower mechanical dynamics) the control is divided in two loops:

• An inner loop for the electrical dynamic,
• An outer loop for the mechanical dynamic.

For speed control, the vector control diagram is shown below:

\(dq\) model

Recall the model in the \(dq\) frame where, the electrical equations are given by: \[ L \frac{di_{dq}}{dt} = v_{dq}-Ri_{dq}-p\omega\mathcal{J} Li_{dq}-e_{dq} \] with \[ e_{dq} =p\omega\mathcal{J} \begin{bmatrix}\phi_f\\0\end{bmatrix}=p\omega \begin{bmatrix}0\\\phi_f\end{bmatrix}, \] and the mechanical equation is given by: \[ J \frac{d\omega}{dt}=\tau_m-f_v\omega -\tau_l, \]

with the electromechanical torque: \[ \tau_m = \frac{3}{2} \frac{1}{\omega} e_{dq}^\intercal i_{dq} = \frac{3}{2}p\phi_fi_q. \]

Electrical dynamic control

The aim here is to control the motor’s electrical dynamic. For this purpose, we consider equation (1). Note that, despite the Clarke and Park transformations, this equation remains non-linear. However, with access to current, position and velocity measurements, it is possible to apply the feedback linearization control (Bodson1993).

Feedback linearization

One poses: \[ v_{dq} = u_{dq} +p\omega\mathcal{J} Li_{dq}+p\omega \begin{bmatrix}0\\\phi_f\end{bmatrix}. \] Applying the control (5) to (1) gives: \[ \frac{di_{dq}}{dt}=\frac{1}{L}u_{dq}-\frac{R}{L}i_{dq}. \] It results in an LTI (Linear Time Invariant) system where the currents \(i_d\) and \(i_q\) are independent. This is why this linearization is often referred to as “decoupling”.

Feedback control with integral action

The control objective is to ensure that \(i_{dq}^\star=i_{dq}^\#\) where \(i_{dq}^\star\) is the steady-state current vector and \(i_{dq}^\#\) is the reference current vector. The principle is to add an integral action in the loop between the error signal and the system (Ogata2010). The control diagram is shown below:

The currents being independent, for \(k\in\{d,q\}\), one poses: \[ \varepsilon_{k} = \int (i_{k}^\# - i_{k}) d\tau, \] the integrator output, leading to: \[ \begin{array}{lcl} \dot{i}_{k} & = & -\frac{R}{L} i_{k} + \frac{1}{L}u_{k}, \\ \dot{\varepsilon_{k}} & = & i_{k}^\# - i_{k}, \\ \end{array} \]

with the control law given by: \[ u_{k} = -g_ki_{k}-g_{I,k}\varepsilon_{k}, \] where \(G_k = \begin{bmatrix}g_k & g_{I,k}\end{bmatrix}\) is the control gain to be chosen.

The system dynamic is described by: \[ \begin{bmatrix} \dot{i}_{k}\\\dot{\varepsilon}_k \end{bmatrix} = \begin{bmatrix} -\frac{R}{L} & 0\\-1 &0 \end{bmatrix} \begin{bmatrix} {i_{k}}\\{\varepsilon}_k \end{bmatrix}+ \begin{bmatrix} \frac{1}{L}\\0 \end{bmatrix}u_{k}+ \begin{bmatrix} 0\\ 1 \end{bmatrix}i_{k}^\#. \]

Leading, with control (9), to the closed loop system given by: \[ \begin{bmatrix} \dot{i}_{k}\\\dot{\varepsilon}_k \end{bmatrix} = \left(\begin{bmatrix} -\frac{R}{L} & 0\\-1 &0 \end{bmatrix} - \begin{bmatrix} \frac{1}{L}\\0 \end{bmatrix} \begin{bmatrix}g_k&g_{I,k}\end{bmatrix}\right)\begin{bmatrix}i_k\\\varepsilon_k\end{bmatrix}+ \begin{bmatrix} 0\\ 1 \end{bmatrix}i_{k}^\#. \]

Closed-loop dynamic therefore depends on the eigenvalues of the matrix: \[ \left(\begin{bmatrix} -\frac{R}{L} & 0\\-1 &0 \end{bmatrix} - \begin{bmatrix} \frac{1}{L}\\0 \end{bmatrix} \begin{bmatrix}g_k&g_{I,k}\end{bmatrix}\right)= \begin{bmatrix} -\frac{R+g_k}{L} & -\frac{g_{I,k}}{L}\\-1 &0 \end{bmatrix}, \] either: \[ {\rm eig}\left( \begin{bmatrix} -\frac{R+g_k}{L} & -\frac{g_{I,k}}{L}\\-1 &0 \end{bmatrix}\right) \Leftrightarrow {\rm det}\left(sI-\begin{bmatrix} -\frac{R+g_k}{L} & -\frac{g_{I,k}}{L}\\-1 &0 \end{bmatrix}\right)=0. \] It leads to a characteristic equation

\[ P(s) = s^2+\frac{g_k+R}{L}s -\frac{g_{I,k}}{L}, \]

to be identified with the classical second order characteristic equation

\[ P(s) = s^2+2\zeta\omega_n s +\omega_n^2 \]

where \(\omega_n\) is the desired closed loop natural frequency and \(\zeta\) the damping coefficient.

Mechanical dynamic control

Assuming the electrical control has been correctly synthesized with respect to frequency separation principle, which means that the closed loop electrical dynamic is faster than the mechanical desired dynamic, then the mechanical dynamic control synthesis can be designed without considering the closed loop electrical system. The control scheme can be simplified as :

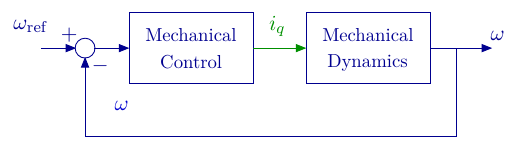
In the absence of load torque \(\tau_l\), from the dynamic equation (3) we obtain : \[ \begin{array}{lcl} \dot{\omega} &=& \frac{3p\phi_f}{2J}i_q-\frac{f_v}{J}\omega.%\\ \end{array} \] The control synthesis is similar than the one proposed for the electrical dynamics with \(\dot\varepsilon_\omega = \omega_{\rm ref}-\omega\) one has: \[ \varepsilon_\omega = \int(\omega_{\rm ref}-\omega) d\tau, \] leading to: \[ \begin{bmatrix} \dot{\omega}\\\dot{\varepsilon_\omega} \end{bmatrix} = \begin{bmatrix} -\frac{f_v}{J} & 0\\-1 &0 \end{bmatrix} \begin{bmatrix} {\omega}\\{\varepsilon_\omega} \end{bmatrix}+ \begin{bmatrix} \frac{3p\phi_f}{2J}\\0 \end{bmatrix}i_q+ \begin{bmatrix} 0\\1 \end{bmatrix}\omega_{\rm ref}, \] with the control: \[ i_q = -g_\omega \omega-g_{I,\omega}\varepsilon_\omega, \] where \(G_\omega =\begin{bmatrix}g_\omega & g_{I,\omega}\end{bmatrix}\) is the control gain to be chosen.

By analogy to the electrical dynamic, it leads to a characteristic equation: \[ P(s) = s^2+\left(\frac{3p\phi_f}{2J} g_\omega+\frac{f_v}{J}\right)s -\frac{3p\phi_f}{2J} g_{I,\omega}, \]

to be identified with the classical second order characteristic equation \[ P(s) = s^2+2\zeta_m\omega_{n,m} s +\omega_{n,m}^2 . \] Note that the control \(i_q\) equation (19) is not a control input. Thus, the control objective will be to provide the current setpoint \(i_q^\#\) to be controlled so that the desired current \(i_q\) is produced by the machine.

References

(Bodson1993) Bodson, M., Chiasson, J.-N., Novotnak, R.-T., & Rekowski, R.-B. (1993). High performance nonlinear feedback control of a permanent magnet stepper motor. IEEE Transactions on Control Systems Technology, 1(1), 5–14. https://doi.org/10.1109/87.221347

(Ogata2010) Ogata, K. (2010). Modern Control Engineering. Prentice Hall.