Motor Control University

Saturation management

Introduction

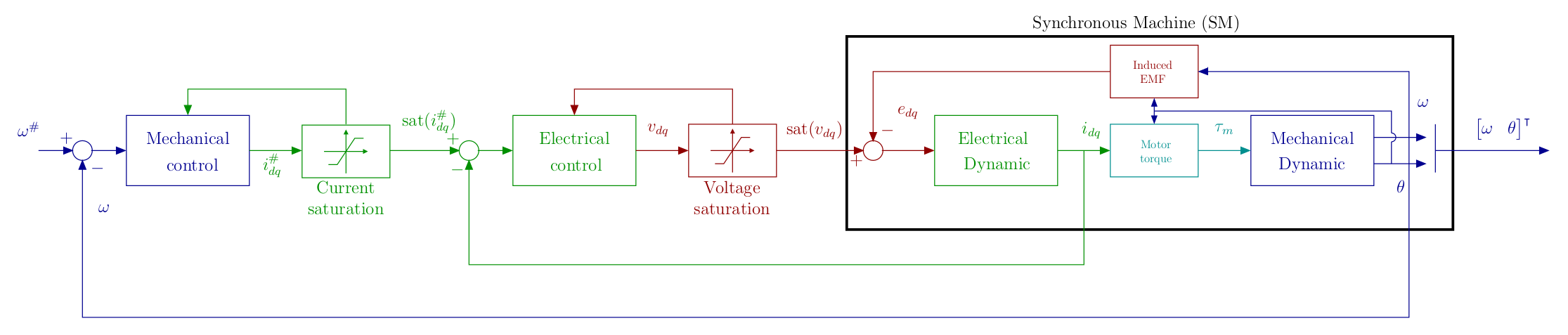
The norm of \(v_{dq}\) is physically constrained, as this quantity cannot exceed a certain positive scalar value \(V_{\rm max}\), which depends on the amplitude of the voltage source and the choice of modulation. As we have seen, sine modulation achieves \(V_{\rm max} = \frac{V_{\rm DC}}{2}\) and space vector modulation \(V_{\rm max} = \frac{V_{\rm DC}}{\sqrt{3}}\). This implies that, the following inequality: \[ ||v_ {dq}|| = \sqrt{v_d^2+v_q^2}\leq V_{\rm max}, \] must always be verified.

The norm of the \(||i_ {dq}||\) current is also limited. At steady state, we have the following constraint: \[ ||i_ {dq}|| = \sqrt{i_d^2+i_q^2}\leq I_{\rm max}. \] In transient operation, current peaks can be accepted by the machine. This constraint depends mainly on the machine’s cooling capacity, which could be damaged if insufficient.

Saturation management strategy

The control scheme proposed above, with its cascaded control loop principle, may appear complicated and increase the number of control gains to be synthesized. However, this scheme has the advantage of allowing good management of both saturations on voltages, which are the control inputs, and currents, which are the system states. In the literature, many works deal with actuator saturation (Tarbouriech2011). Much less is devoted to state saturation.

In order to saturate the norm of voltages \(v_{dq}\) and currents \(i_{dq}\), the solution adopted here is to maintain the direction of the vectors. In other words, to maintain the same proportion along the \(d\) and \(q\) axes. This strategy is illustrated below:

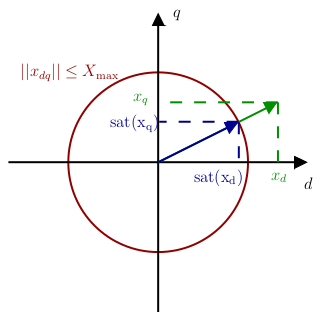
For any vector \(x_{dq}\), its saturated output \(\rm sat{(x_{dq})}\), will be expressed by: \[ \rm sat{(x_{dq})} = \left\{ \begin{array}{ll} x_{dq} & {\rm if } \quad ||x_{dq}||\leq X_{\rm max},\\ \frac{x_{dq}}{||x_{dq}||}X_{\rm max} & {\rm otherwise }. \end{array} \right. \] Remark: In some cases, favoring one axis over the other can be advantageous. For example, in the case of currents, the current along the \(q\) axis is proportional to the motor torque to be supplied and could be favored (Beciu2018).

Anti-wind-up strategy

The saturation of an actuator in a control loop including an integral action is a classic problem (Tarbouriech2020). When the input saturates, the integral term continues to load when it doesn’t has to. The integrator’s output is then said to be “windup”. Various algorithms have been proposed to deal with this problem (Tarbouriech2009, Zaccarian2011). However, most of them rely on additional tuning parameters. To date, solving real-time convex optimization problems for anti-windup gain synthesis has not been studied in our approach. We therefore propose, here, an easy-to-implement solution, with no additional gain to adjust (Astrom2006), shown on figure below:

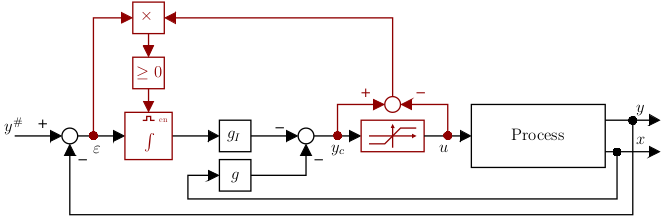
The integral action is activated (“enabled”) if the controller output \(y_c\) is not saturated, or if \(y_c\) is saturated but the error to be integrated would help the controller to leave saturation. When the integral action is deactivated, the value of its output is maintained. In the literature, this solution is known as conditional integration or integrator clamping (Astrom2006).

Remark: In practice, the strategy was adapted to provide dynamic current strategy. Indeed, at high speed, current limits may reduce with respect to voltage saturation has shown in the above paragraph Field-weakening.

References

(Astrom2006) Astrom, K.-J., & Hagglund, T. (2006). Advanced PID control. ISA. https://cds.cern.ch/record/1514097

(Beciu2018) A. Beciu, & G. Valmorbida. (2018). Anti-Windup Design for Synchronous Machines. International Workshop on Robust LPV Control Techniques and Anti-Windup Design.

(Verl1998) Verl, A., & Bodson, M. (1998). Torque Maximization for Permanent Magnet Synchronous Motors. IEEE Transactions on Control Systems Technology, 6(6), 740–745.

(Tarbouriech2009)Tarbouriech, S., & Turner, M. (2009). Anti-windup design: an overview of some recent advances and open problems. IET Control Theory & Applications, 3(1), 1-19(18).

(Tarbouriech2011) Tarbouriech, S., Garcia, G., Gomes da Silva Jr., J.-M., & Queinnec, I. (2011). Stability and Stabilization of Linear Systems with Saturating Actuators. Springer-Verlag London.

(Tarbouriech2020) Tarbouriech, S., & Queinnec, I. (2020). Tour d’horizon sur les techniques anti-windup pour les systèmes saturés Commande anti-windup. Techniques de l’ingénieur.

(Zaccarian2011) Zaccarian, L., & Teel, A.-R. (2011). Modern anti-windup synthesis: control augmentation for actuator saturation. Princeton University Press.