Motor Control University

Transformations

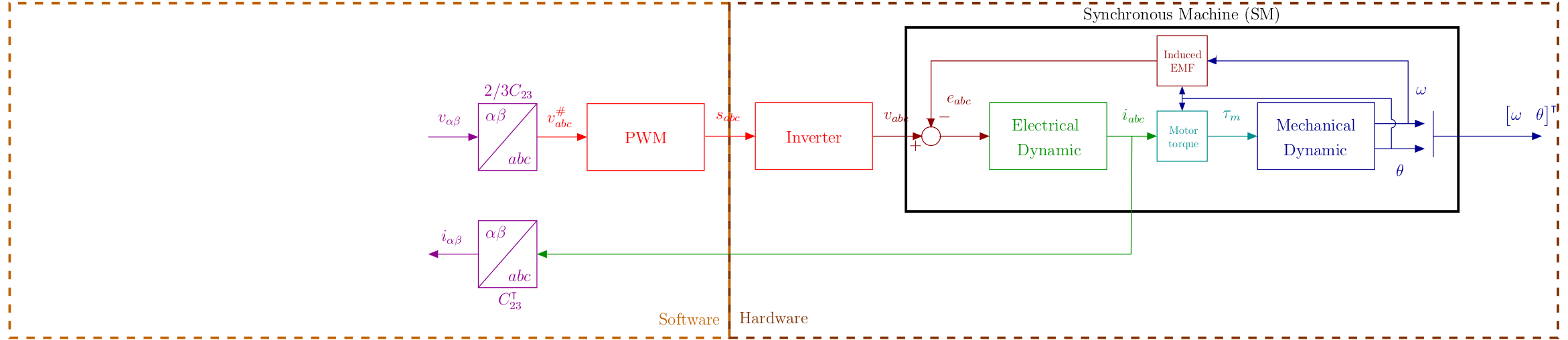
While in the modeling page a three-phase mathematical model of the motor was introduced, in this section, are introduced Clarke and Park transformation, to define a two-phase equivalent model of the motor (Glumineau2015). Using these tranformations leads to a simplified the model for control purposes.

Clarke transformation : 2-phases equivalent representation

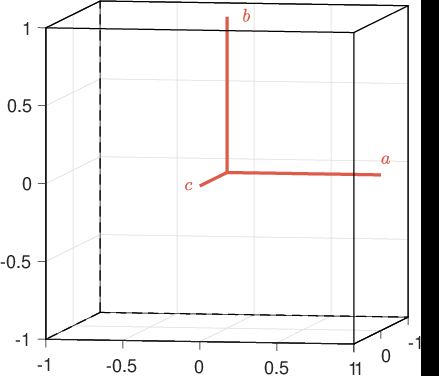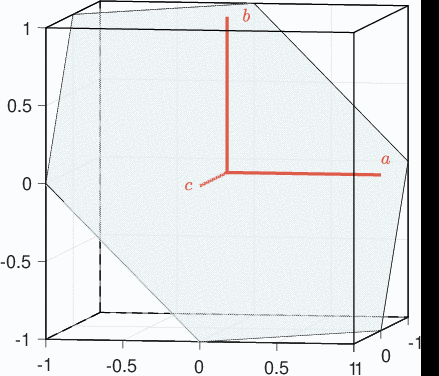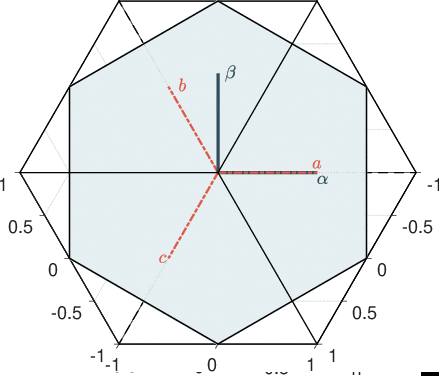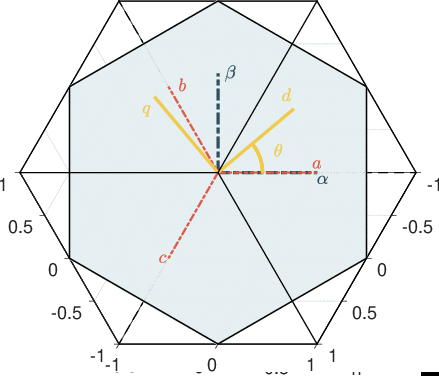
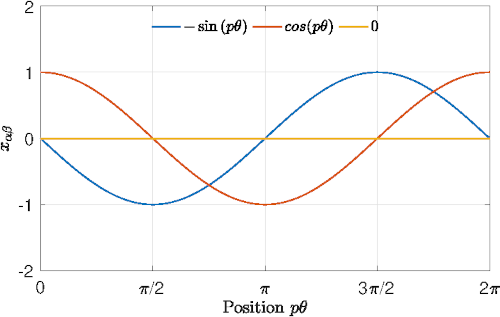
Under the assumption of balanced motor one has \(x_a+x_b+x_c = 0\). Motor equations can thus be transformed into a 2-phases equivalent representation using Clarke transformation. Note \(C_{23}\), the Clarke’s submatrix for transition from three-phase to two-phase systems \(\alpha\beta\) : \[ \begin{equation} C_{23} = \left[ \begin{matrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{matrix} \right], \label{eq:Clarke} \end{equation} \] such that \[ x_{\alpha\beta}=\frac{2}{3}C_{23}x_{abc}, \] and \[ x_{abc}=C_{23}^\intercal x_{\alpha\beta}. \] The electrical equations leads to: \[ \label{eq:modeleab} L \frac{di_{\alpha\beta}}{dt} = v_{\alpha\beta}-R i_{\alpha\beta}-e_{\alpha\beta} \] with \[ e_{\alpha\beta} = p\omega\phi_f \begin{bmatrix} -\sin\left(p\theta\right)\\ \cos(p\theta) \end{bmatrix}. \] The electromechanical torque in this frame is given by : \[ \tau_m = \frac{3}{2} \frac{1}{\omega} e_{\alpha\beta}^\intercal i_{\alpha\beta}. \]

Park transformation : \(d-q\) rotating frame

In the previous model, voltages and currents varies at high frequency (p times the rotational frequency). To avoid sinus terms Park transformation is used (Park29).

The Park transform is a rotation matrix \(P(\theta)\) from \(\alpha\beta\) axes to \(dq\) axes. One as \[ x_{dq} = P(\theta) x_{\alpha\beta}, \]

\[ x_{\alpha\beta} = P(\theta)^{-1} x_{dq}, \] where: \[ P(\theta) =\left[ \begin{matrix} \cos(p\theta) & \sin(p\theta)\\ -\sin(p\theta) & \cos(p\theta)\\ \end{matrix} \right]. \]

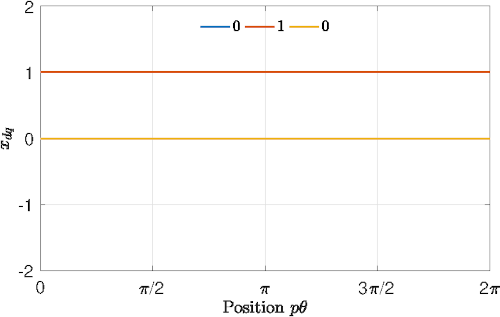
The electrical equations leads to: \[ L \frac{di_{dq}}{dt} = v_{dq}-Ri_{dq}-p\omega\mathcal{J} Li_{dq}-e_{dq} \] with \[ e_{dq} =p\omega\mathcal{J} \begin{bmatrix}\phi_f\\0\end{bmatrix}=p\omega \begin{bmatrix}0\\\phi_f\end{bmatrix}. \] The electromechanical torque in this frame is given by : \[ \tau_m = \frac{3}{2} \frac{1}{\omega} e_{dq}^\intercal i_{dq} = \frac{3}{2}p\phi_fi_q. \]

Equivalent model in the \(dq\) frame

The equivalent model in the \(dq\) frame is adapted for the control stategy prosed in the next section.

References :

(Glumineau2015) Glumineau, A., & de Leon Morales, J. (2015). Sensorless AC Electric Motor Control (Advances i). Springer International Publishing. https://doi.org/10.1007/978-3-319-14586-0

(Park29) Park, R.-H. (1929). Two-reaction theory of synchronous machines generalized method of analysis-part I. Transactions of the American Institute of Electrical Engineers, 48(3), 716–727. https://doi.org/10.1109/T-AIEE.1929.5055275